One of many extra thrilling purposes of decentralized computing which have aroused a substantial quantity of curiosity prior to now yr is the idea of an incentivized decentralized on-line file storage system. At present, if you would like your recordsdata or knowledge securely backed up “within the cloud”, you may have three decisions – (1) add them to your individual servers, (2) use a centralized service like Google Drive or Dropbox or (3) use an current decentralized file system like Freenet. These approaches all have their very own faults; the primary has a excessive setup and upkeep value, the second depends on a single trusted get together and sometimes entails heavy value markups, and the third is gradual and really restricted within the quantity of house that it permits every consumer as a result of it depends on customers to volunteer storage. Incentivized file storage protocols have the potential to supply a fourth method, offering a a lot greater amount of storage and high quality of service by incentivizing actors to take part with out introducing centralization.
Quite a few platforms, together with StorJ, Maidsafe, to some extent Permacoin, and Filecoin, try to deal with this downside, and the issue appears easy within the sense that every one the instruments are both already there or en path to being constructed, and all we’d like is the implementation. Nevertheless, there’s one a part of the issue that’s significantly vital: how will we correctly introduce redundancy? Redundancy is essential to safety; particularly in a decentralized community that will probably be extremely populated by novice and informal customers, we completely can not depend on any single node to remain on-line. We may merely replicate the information, having just a few nodes every retailer a separate copy, however the query is: can we do higher? Because it seems, we completely can.
Merkle Timber and Problem-Response Protocols
Earlier than we get into the nitty gritty of redundancy, we are going to first cowl the better half: how will we create at the least a primary system that can incentivize at the least one get together to carry onto a file? With out incentivization, the issue is straightforward; you merely add the file, look forward to different customers to obtain it, after which while you want it once more you can also make a request querying for the file by hash. If we need to introduce incentivization, the issue turns into considerably tougher – however, within the grand scheme of issues, nonetheless not too laborious.
Within the context of file storage, there are two sorts of actions you could incentivize. The primary is the precise act of sending the file over to you while you request it. That is simple to do; the perfect technique is an easy tit-for-tat recreation the place the sender sends over 32 kilobytes, you ship over 0.0001 cash, the sender sends over one other 32 kilobytes, and so forth. Be aware that for very massive recordsdata with out redundancy this technique is weak to extortion assaults – very often, 99.99% of a file is ineffective to you with out the final 0.01%, so the storer has the chance to extort you by asking for a really excessive payout for the final block. The cleverest repair to this downside is definitely to make the file itself redundant, utilizing a particular sort of encoding to develop the file by, say, 11.11% in order that any 90% of this prolonged file can be utilized to get better the unique, after which hiding the precise redundancy share from the storer; nevertheless, because it seems we are going to focus on an algorithm similar to this for a distinct objective later, so for now, merely settle for that this downside has been solved.
The second act that we will incentivize is the act of holding onto the file and storing it for the long run. This downside is considerably tougher – how will you show that you’re storing a file with out truly transferring the entire thing? Fortuitously, there’s a resolution that’s not too troublesome to implement, utilizing what has now hopefully established a well-recognized status because the cryptoeconomist’s finest pal: Merkle timber.

Properly, Patricia Merkle could be higher in some instances, to be exact. Athough right here the plain previous unique Merkle will do.
n = 2^okayfor some
okay(the padding step is avoidable, however it makes the algorithm less complicated to code and clarify). Then, we construct the tree. Rename the
nchunks that we acquired
chunk[n]to
chunk[2n-1], after which rebuild chunks
1to
n-1with the next rule:
chunk[i] = sha3([chunk[2*i], chunk[2*i+1]]). This allows you to calculate chunks
n/2to
n-1, then
n/4to
n/2 - 1, and so forth going up the tree till there’s one “root”,
chunk[1].
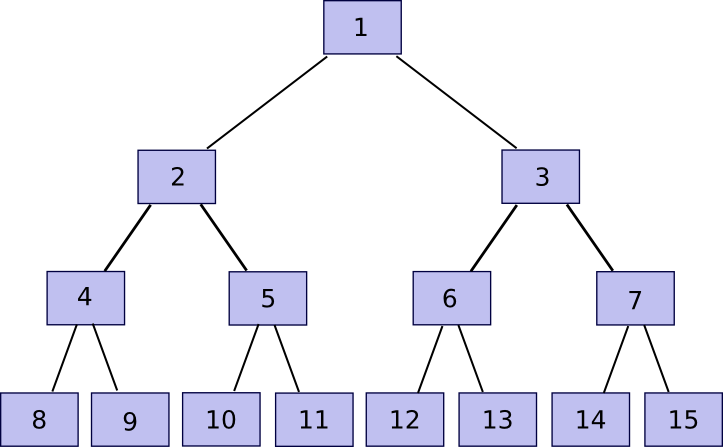
Now, notice that when you retailer solely the foundation, and neglect about chunk[2] … chunk[2n-1], the entity storing these different chunks can show to you that they’ve any explicit chunk with just a few hundred bytes of information. The algorithm is comparatively easy. First, we outline a operate accomplice(n) which supplies n-1 if n is odd, in any other case n+1 – briefly, given a piece discover the chunk that it’s hashed along with with a view to produce the mother or father chunk. Then, if you wish to show possession of chunk[k] with n <= okay <= 2n-1 (ie. any a part of the unique file), submit chunk[partner(k)], chunk[partner(k/2)] (division right here is assumed to spherical down, so eg. 11 / 2 = 5), chunk[partner(k/4)] and so forth right down to chunk[1], alongside the precise chunk[k]. Basically, we’re offering the whole “department” of the tree going up from that node all the best way to the foundation. The verifier will then take chunk[k] and chunk[partner(k)] and use that to rebuild chunk[k/2], use that and chunk[partner(k/2)] to rebuild chunk[k/4] and so forth till the verifier will get to chunk[1], the foundation of the tree. If the foundation matches, then the proof is okay; in any other case it is not.
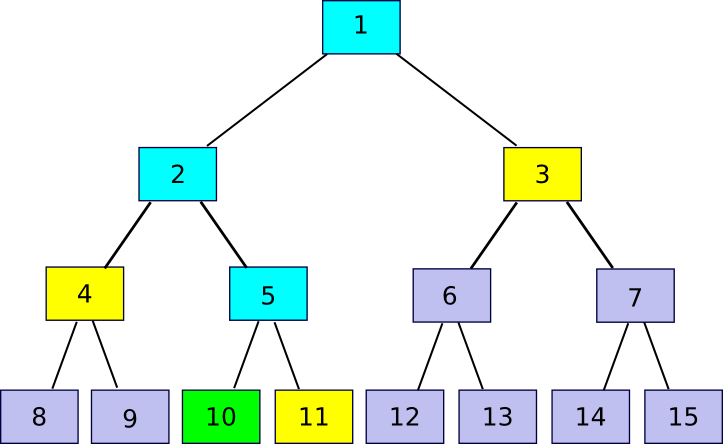
11 = accomplice(10)), 4 (
4 = accomplice(10/2)) and three (
3 = accomplice(10/4)). The verification course of entails beginning off with chunk 10, utilizing every accomplice chunk in flip to recompute first chunk 5, then chunk 2, then chunk 1, and seeing if chunk 1 matches the worth that the verifier had already saved as the foundation of the file.
Be aware that the proof implicitly consists of the index – generally you should add the accomplice chunk on the precise earlier than hashing and generally on the left, and if the index used to confirm the proof is completely different then the proof won’t match. Thus, if I ask for a proof of piece 422, and also you as a substitute present even a legitimate proof of piece 587, I’ll discover that one thing is incorrect. Additionally, there is no such thing as a method to supply a proof with out possession of the whole related part of the Merkle tree; when you attempt to go off faux knowledge, in some unspecified time in the future the hashes will mismatch and the ultimate root will probably be completely different.
Now, let’s go over the protocol. I assemble a Merkle tree out of the file as described above, and add this to some get together. Then, each 12 hours, I choose a random quantity in [0, 2^k-1] and submit that quantity as a problem. If the storer replies again with a Merkle tree proof, then I confirm the proof and whether it is appropriate ship 0.001 BTC (or ETH, or storjcoin, or no matter different token is used). If I obtain no proof or an invalid proof, then I don’t ship BTC. If the storer shops the whole file, they’ll succeed 100% of the time, in the event that they retailer 50% of the file they’ll succeed 50% of the time, and so forth. If we need to make it all-or-nothing, then we will merely require the storer to resolve ten consecutive proofs with a view to get a reward. The storer can nonetheless get away with storing 99%, however then we benefit from the identical redundant coding technique that I discussed above and can describe beneath to make 90% of the file ample in any case.
One concern that you will have at this level is privateness – when you use a cryptographic protocol to let any node receives a commission for storing your file, would that not imply that your recordsdata are unfold across the web in order that anybody can doubtlessly entry them? Fortuitously the reply to that is easy: encrypt the file earlier than sending it out. From this level on, we’ll assume that every one knowledge is encrypted, and ignore privateness as a result of the presence of encryption resolves that concern virtually utterly (the “virtually” being that the scale of the file, and the occasions at which you entry the file, are nonetheless public).
Seeking to Decentralize
So now now we have a protocol for paying individuals to retailer your knowledge; the algorithm may even be made trust-free by placing it into an Ethereum contract, utilizing
block.prevhash as a supply of random knowledge to generate the challenges. Now let’s go to the following step: determining the best way to decentralize the storage and add redundancy. The best option to decentralize is straightforward replication: as a substitute of 1 node storing one copy of the file, we will have 5 nodes storing one copy every. Nevertheless, if we merely observe the naive protocol above, now we have an issue: one node can fake to be 5 nodes and accumulate a 5x return. A fast repair to that is to encrypt the file 5 occasions, utilizing 5 completely different keys; this makes the 5 equivalent copies indistinguishable from 5 completely different recordsdata, so a storer won’t be able to note that the 5 recordsdata are the identical and retailer them as soon as however declare a 5x reward.
However even right here now we have two issues. First, there is no such thing as a option to confirm that the 5 copies of the file are saved by 5 separate customers. If you wish to have your file backed up by a decentralized cloud, you’re paying for the service of decentralization; it makes the protocol have a lot much less utility if all 5 customers are literally storing every part via Google and Amazon. That is truly a tough downside; though encrypting the file 5 occasions and pretending that you’re storing 5 completely different recordsdata will stop a single actor from amassing a 5x reward with 1x storage, it can not stop an actor from amassing a 5x reward with 5x storage, and economies of scale imply even that scenario will probably be fascinating from the perspective of some storers. Second, there’s the problem that you’re taking a big overhead, and particularly taking the false-redundancy concern into consideration you’re actually not getting that a lot redundancy from it – for instance, if a single node has a 50% probability of being offline (fairly cheap if we’re speaking a few community of recordsdata being saved within the spare house on individuals’s laborious drives), then you may have a 3.125% probability at any level that the file will probably be inaccessible outright.
There may be one resolution to the primary downside, though it’s imperfect and it is not clear if the advantages are price it. The concept is to make use of a mixture of proof of stake and a protocol known as “proof of custody” – proof of simultaneous possession of a file and a personal key. If you wish to retailer your file, the concept is to randomly choose some variety of stakeholders in some forex, weighting the likelihood of choice by the variety of cash that they’ve. Implementing this in an Ethereum contract may contain having individuals deposit ether within the contract (keep in mind, deposits are trust-free right here if the contract offers a option to withdraw) after which giving every account a likelihood proportional to its deposit. These stakeholders will then obtain the chance to retailer the file. Then, as a substitute of the easy Merkle tree verify described within the earlier part, the proof of custody protocol is used.
The proof of custody protocol has the profit that it’s non-outsourceable – there is no such thing as a option to put the file onto a server with out giving the server entry to your non-public key on the identical time. Which means, at the least in idea, customers will probably be a lot much less inclined to retailer massive portions of recordsdata on centralized “cloud” computing methods. After all, the protocol accomplishes this at the price of a lot greater verification overhead, in order that leaves open the query: do we wish the verification overhead of proof of custody, or the storage overhead of getting additional redundant copies simply in case?
M of N
No matter whether or not proof of custody is a good suggestion, the following step is to see if we will perform a little higher with redundancy than the naive replication paradigm. First, let’s analyze how good the naive replication paradigm is. Suppose that every node is offered 50% of the time, and you’re keen to take 4x overhead. In these instances, the possibility of failure is
0.5 ^ 4 = 0.0625 – a somewhat excessive worth in comparison with the “4 nines” (ie. 99.99% uptime) provided by centralized companies (some centralized companies provide 5 – 6 nines, however purely due to Talebian black swan concerns any guarantees over three nines can usually be thought-about bunk; as a result of decentralized networks don’t depend upon the existence or actions of any particular firm or hopefully any particular software program package deal, nevertheless, decentralized methods arguably truly can promise one thing like 4 nines legitimately). If we assume that almost all of the community will probably be quasi-professional miners, then we will scale back the unavailability share to one thing like 10%, through which case we truly do get 4 nines, however it’s higher to imagine the extra pessimistic case.
What we thus want is a few sort of M-of-N protocol, very like multisig for Bitcoin. So let’s describe our dream protocol first, and fear about whether or not it is possible later. Suppose that now we have a file of 1 GB, and we need to “multisig” it right into a 20-of-60 setup. We break up the file up into 60 chunks, every 50 MB every (ie. 3 GB whole), such that any 20 of these chunks suffice to reconstruct the unique. That is information-theoretically optimum; you’ll be able to’t reconstruct a gigabyte out of lower than a gigabyte, however reconstructing a gigabyte out of a gigabyte is totally potential. If now we have this type of protocol, we will use it to separate every file up into 60 items, encrypt the 60 chunks individually to make them appear to be impartial recordsdata, and use an incentivized file storage protocol on every one individually.
Now, right here comes the enjoyable half: such a protocol truly exists. On this subsequent a part of the article, we’re going to describe a bit of math that’s alternately known as both “secret sharing” or “erasure coding” relying on its utility; the algorithm used for each these names is mainly the identical excluding one implementation element. To begin off, we are going to recall a easy perception: two factors make a line.
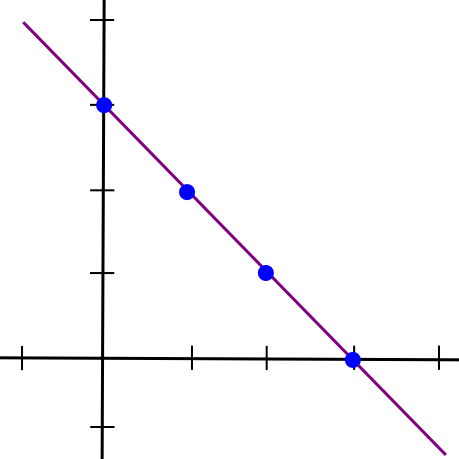
x = 1and the second half because the y coordinate of the road at
x = 2, draw the road, and take factors at
x = 3,
x = 4, and so forth. Any two items can then be used to reconstruct the road, and from there derive the y coordinates at
x = 1and
x = 2 to get the file again.
Mathematically, there are two methods of doing this. The primary is a comparatively easy strategy involving a system of linear equations. Suppose that we file we need to break up up is the quantity “1321”. The left half is 13, the precise half is 21, so the road joins (1, 13) and (2, 21). If we need to decide the slope and y-intercept of the road, we will simply remedy the system of linear equations:
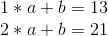
Subtract the primary equation from the second, and also you get:
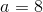
After which plug that into the primary equation, and get:
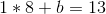
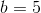
So now we have our equation, y = 8 * x + 5. We are able to now generate new factors: (3, 29), (4, 37), and so forth. And from any two of these factors we will get better the unique equation.
Now, let’s go one step additional, and generalize this into m-of-n. Because it seems, it is extra sophisticated however not too troublesome. We all know that two factors make a line. We additionally know that three factors make a parabola:
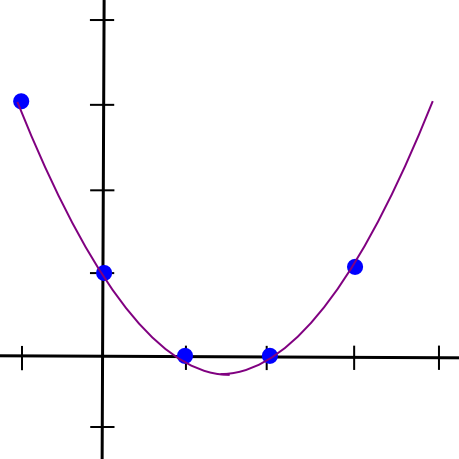
x = 1, 2, 3, and take additional factors on the parabola as extra items. If we wish 4-of-n, we use a cubic polynomial as a substitute. Let’s undergo that latter case; we nonetheless hold our unique file, “1321”, however we’ll break up it up utilizing 4-of-7 as a substitute. Our 4 factors are
(1, 1),
(2, 3),
(3, 2),
(4, 1). So now we have:
Eek! Properly, let’s, uh, begin subtracting. We’ll subtract equation 1 from equation 2, 2 from 3, and three from 4, to cut back 4 equations to a few, after which repeat that course of repeatedly.
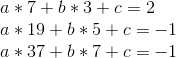
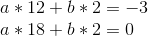
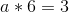
So a = 1/2. Now, we unravel the onion, and get:
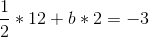
So b = -9/2, after which:
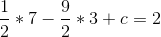
So c = 12, after which:
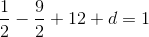
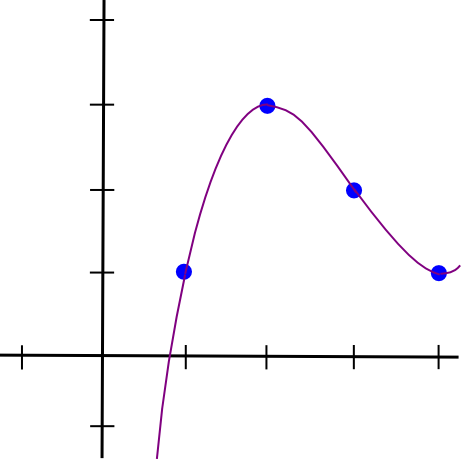
So a = 0.5, b = -4.5, c = 12, d = -7. Here is the beautiful polynomial visualized:
I created a Python utility that can assist you do that (this utility additionally does different extra superior stuff, however we’ll get into that later); you’ll be able to obtain it right here. In the event you wished to resolve the equations shortly, you’ll simply sort in:
> import share > share.sys_solve([[1.0, 1.0, 1.0, 1.0, -1.0], [8.0, 4.0, 2.0, 1.0, -3.0], [27.0, 9.0, 3.0, 1.0, -2.0], [64.0, 16.0, 4.0, 1.0, -1.0]]) [0.5, -4.5, 12.0, -7.0]
Be aware that placing the values in as floating level is important; when you use integers Python’s integer division will screw issues up.
Now, we’ll cowl the better option to do it, Lagrange interpolation. The concept right here could be very intelligent: we give you a cubic polynomial whose worth is 1 at x = 1 and 0 at x = 2, 3, 4, and do the identical for each different x coordinate. Then, we multiply and add the polynomials collectively; for instance, to match (1, 3, 2, 1) we merely take 1x the polynomial that passes via (1, 0, 0, 0), 3x the polynomial via (0, 1, 0, 0), 2x the polynomial via (0, 0, 1, 0) and 1x the polynomial via (0, 0, 0, 1) after which add these polynomials collectively to get the polynomal via (1, 3, 2, 1) (notice that I stated the polynomial passing via (1, 3, 2, 1); the trick works as a result of 4 factors outline a cubic polynomial uniquely). This may not appear simpler, as a result of the one method now we have of becoming polynomials to factors to far is the cumbersome process above, however happily, we even have an express building for it:
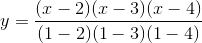
At x = 1, discover that the highest and backside are equivalent, so the worth is 1. At x = 2, 3, 4, nevertheless, one of many phrases on the highest is zero, so the worth is zero. Multiplying up the polynomials takes quadratic time (ie. ~16 steps for 4 equations), whereas our earlier process took cubic time (ie. ~64 steps for 4 equations), so it is a substantial enchancment particularly as soon as we begin speaking about bigger splits like 20-of-60. The python utility helps this algorithm too:
> import share > share.lagrange_interp([1.0, 3.0, 2.0, 1.0], [1.0, 2.0, 3.0, 4.0]) [-7.0, 12.000000000000002, -4.5, 0.4999999999999999]
The primary argument is the y coordinates, the second is the x coordinates. Be aware the other order right here; the code within the python module places the lower-order coefficients of the polynomial first. And eventually, let’s get our extra shares:
> share.eval_poly_at([-7.0, 12.0, -4.5, 0.5], 5) 3.0 > share.eval_poly_at([-7.0, 12.0, -4.5, 0.5], 6) 11.0 > share.eval_poly_at([-7.0, 12.0, -4.5, 0.5], 7) 28.0
So right here instantly we will see two issues. First, it seems like computerized floating level numbers aren’t infinitely exact in any case; the 12 became 12.000000000000002. Second, the chunks begin getting massive as we transfer additional out; at x = 10, it goes as much as 163. That is considerably breaking the promise that the quantity of information you should get better the file is identical dimension as the unique file; if we lose x = 1, 2, 3, 4 then you definitely want 8 digits to get the unique values again and never 4. These are each critical points, and ones that we’ll resolve with some extra mathematical cleverness later, however we’ll go away them apart for now.
Even with these points remaining, now we have mainly achieved victory, so let’s calculate our spoils. If we use a 20-of-60 break up, and every node is on-line 50% of the time, then we will use combinatorics – particularly, the binomial distribution system – to compute the likelihood that our knowledge is okay. First, to set issues up:
> def fac(n): return 1 if n==0 else n * fac(n-1) > def select(n,okay): return fac(n) / fac(okay) / fac(n-k) > def prob(n,okay,p): return select(n,okay) * p ** okay * (1-p) ** (n-k)
The final system computes the likelihood that precisely okay servers out of n will probably be on-line if every particular person server has a likelihood p of being on-line. Now, we’ll do:
> sum([prob(60, k, 0.5) for k in range(0, 20)]) 0.0031088013296633353
99.7% uptime with solely 3x redundancy – a great step up from the 87.5% uptime that 3x redundancy would have given us had easy replication been the one instrument in our toolkit. If we crank the redundancy as much as 4x, then we get six nines, and we will cease there as a result of the likelihood both Ethereum or the whole web will crash outright is larger than 0.0001% anyway (in reality, you are extra prone to die tomorrow). Oh, and if we assume every machine has 90% uptime (ie. hobbyist “farmers”), then with a 1.5x-redundant 20-of-30 protocol we get a fully overkill twelve nines. Popularity methods can be utilized to maintain monitor of how typically every node is on-line.
Coping with Errors
We’ll spend the remainder of this text discussing three extensions to this scheme. The primary is a priority that you will have left out studying the above description, however one which is nonetheless vital: what occurs if some node tries to actively cheat? The algorithm above can get better the unique knowledge of a 20-of-60 break up from any 20 items, however what if one of many knowledge suppliers is evil and tries to supply faux knowledge to screw with the algorithm. The assault vector is a somewhat compelling one:
> share.lagrange_interp([1.0, 3.0, 2.0, 5.0], [1.0, 2.0, 3.0, 4.0]) [-11.0, 19.333333333333336, -8.5, 1.1666666666666665]
Taking the 4 factors of the above polynomial, however altering the final worth to five, provides a totally completely different consequence. There are two methods of coping with this downside. One is the apparent method, and the opposite is the mathematically intelligent method. The apparent method is apparent: when splitting a file, hold the hash of every chunk, and examine the chunk towards the hash when receiving it. Chunks that don’t match their hashes are to be discarded.
The intelligent method is considerably extra intelligent; it entails some spooky not-quite-moon-math known as the Berlekamp-Welch algorithm. The concept is that as a substitute of becoming only one polynomial, P, we think about into existence two polynomials, Q and E, such that Q(x) = P(x) * E(x), and attempt to remedy for each Q and E on the identical time. Then, we compute P = Q / E. The concept is that if the equation holds true, then for all x both P(x) = Q(x) / E(x) or E(x) = 0; therefore, other than computing the unique polynomial we magically isolate what the errors are. I will not go into an instance right here; the Wikipedia article has a wonderfully respectable one, and you’ll strive it your self with:
> map(lambda x: share.eval_poly_at([-7.0, 12.0, -4.5, 0.5], x), [1, 2, 3, 4, 5, 6]) [1.0, 3.0, 2.0, 1.0, 3.0, 11.0] > share.berlekamp_welch_attempt([1.0, 3.0, 18018.0, 1.0, 3.0, 11.0], [1, 2, 3, 4, 5, 6], 3) [-7.0, 12.0, -4.5, 0.5] > share.berlekamp_welch_attempt([1.0, 3.0, 2.0, 1.0, 3.0, 0.0], [1, 2, 3, 4, 5, 6], 3) [-7.0, 12.0, -4.5, 0.5]
Now, as I discussed, this mathematical trickery will not be actually all that wanted for file storage; the less complicated strategy of storing hashes and discarding any piece that doesn’t match the recorded hash works simply fantastic. However it’s by the way fairly helpful for an additional utility: self-healing Bitcoin addresses. Bitcoin has a base58check encoding algorithm, which can be utilized to detect when a Bitcoin deal with has been mistyped and returns an error so you don’t by chance ship hundreds of {dollars} into the abyss. Nevertheless, utilizing what we all know, we will truly do higher and make an algorithm which not solely detects mistypes but in addition truly corrects the errors on the fly. We do not use any sort of intelligent deal with encoding for Ethereum as a result of we choose to encourage use of identify registry-based options, but when an deal with encoding scheme was demanded one thing like this could possibly be used.
Finite Fields
Now, we get again to the second downside: as soon as our x coordinates get somewhat greater, the y coordinates begin capturing off in a short time towards infinity. To resolve this, what we’re going to do is nothing in need of utterly redefining the principles of arithmetic as we all know them. Particularly, let’s redefine our arithmetic operations as:
a + b := (a + b) % 11 a - b := (a - b) % 11 a * b := (a * b) % 11 a / b := (a * b ** 9) % 11
That “p.c” signal there’s “modulo”, ie. “take the rest of dividing that vaue by 11”, so now we have
7 + 5 = 1,
6 * 6 = 3(and its corollary
3 / 6 = 6), and so forth. We at the moment are solely allowed to take care of the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. The shocking factor is that, whilst we do that, the entire guidelines about conventional arithmetic nonetheless maintain with our new arithmetic;
(a * b) * c = a * (b * c),
(a + b) * c = (a * c) + (b * c),
a / b * b = aif
b != 0,
(a^2 - b^2) = (a - b)*(a + b), and so forth. Thus, we will merely take the algebra behind our polynomial encoding that we used above, and transplant it over into the brand new system. Despite the fact that the instinct of a polynomial curve is totally borked – we’re now coping with summary mathematical objects and never something resembling precise factors on a aircraft – as a result of our new algebra is self-consistent, the formulation nonetheless work, and that is what counts.
> e = share.mkModuloClass(11) > P = share.lagrange_interp(map(e, [1, 3, 2, 1]), map(e, [1, 2, 3, 4])) > P [4, 1, 1, 6] > map(lambda x: share.eval_poly_at(map(e, P), e(x)), vary(1, 9)) [1, 3, 2, 1, 3, 0, 6, 2] > share.berlekamp_welch_attempt(map(e, [1, 9, 9, 1, 3, 0, 6, 2]), map(e, [1, 2, 3, 4, 5, 6, 7, 8]), 3) [4, 1, 1, 6]
The “
map(e, [v1, v2, v3])” is used to transform extraordinary integers into parts on this new area; the software program library consists of an implementation of our loopy modulo 11 numbers that interfaces with arithmetic operators seamlessly so we will merely swap them in (eg.
print e(6) * e(6)returns
3). You’ll be able to see that every part nonetheless works – besides that now, as a result of our new definitions of addition, subtraction, multiplication and division all the time return integers in
[0 ... 10] we by no means want to fret about both floating level imprecision or the numbers increasing because the x coordinate will get too excessive.
Now, in actuality these comparatively easy modulo finite fields should not what are often utilized in error-correcting codes; the commonly most popular building is one thing known as a Galois area (technically, any area with a finite variety of parts is a Galois area, however generally the time period is used particularly to check with polynomial-based fields as we are going to describe right here). The concept is that the weather within the area at the moment are polynomials, the place the coefficients are themselves values within the area of integers modulo 2 (ie. a + b := (a + b) % 2, and so forth). Including and subtracting work as usually, however multiplying is itself modulo a polynomial, particularly x^8 + x^4 + x^3 + x + 1. This somewhat sophisticated multilayered building lets us have a area with precisely 256 parts, so we will conveniently retailer each ingredient in a single byte and each byte as one ingredient. If we need to work on chunks of many bytes at a time, we merely apply the scheme in parallel (ie. if every chunk is 1024 bytes, decide 10 polynomials, one for every byte, lengthen them individually, and mix the values at every x coordinate to get the chunk there).
However it isn’t vital to know the precise workings of this; the salient level is that we will redefine +, –, * and / in such a method that they’re nonetheless absolutely self-consistent however all the time take and output bytes.
Going Multidimensional: The Self-Therapeutic Dice
Now, we’re utilizing finite fields, and we will take care of errors, however one concern nonetheless stays: what occurs when nodes do go down? At any cut-off date, you’ll be able to rely on 50% of the nodes storing your file staying on-line, however what you can’t rely on is identical nodes staying on-line perpetually – ultimately, just a few nodes are going to drop out, then just a few extra, then just a few extra, till ultimately there should not sufficient of the unique nodes left on-line. How will we struggle this gradual attrition? One technique is that you may merely watch the contracts which are rewarding every particular person file storage occasion, seeing when some cease paying out rewards, after which re-upload the file. Nevertheless, there’s a downside: with a view to re-upload the file, you should reconstruct the file in its entirety, a doubtlessly troublesome job for the multi-gigabyte motion pictures that at the moment are wanted to fulfill individuals’s seemingly insatiable wishes for multi-thousand pixel decision. Moreover, ideally we want the community to have the ability to heal itself with out requiring lively involvement from a centralized supply, even the proprietor of the recordsdata.
Fortuitously, such an algorithm exists, and all we have to accomplish it’s a intelligent extension of the error correcting codes that we described above. The basic concept that we will depend on is the truth that polynomial error correcting codes are “linear”, a mathematical time period which mainly signifies that it interoperates properly with multiplication and addition. For instance, take into account:
> share.lagrange_interp([1.0, 3.0, 2.0, 1.0], [1.0, 2.0, 3.0, 4.0]) [-7.0, 12.000000000000002, -4.5, 0.4999999999999999] > share.lagrange_interp([10.0, 5.0, 5.0, 10.0], [1.0, 2.0, 3.0, 4.0]) [20.0, -12.5, 2.5, 0.0] > share.lagrange_interp([11.0, 8.0, 7.0, 11.0], [1.0, 2.0, 3.0, 4.0]) [13.0, -0.5, -2.0, 0.5000000000000002] > share.lagrange_interp([22.0, 16.0, 14.0, 22.0], [1.0, 2.0, 3.0, 4.0]) [26.0, -1.0, -4.0, 1.0000000000000004]
See how the enter to the third interpolation is the sum of the inputs to the primary two, and the output finally ends up being the sum of the primary two outputs, after which once we double the enter it additionally doubles the output. So what’s the good thing about this? Properly, this is the intelligent trick. Erasure cording is itself a linear system; it depends solely on multiplication and addition. Therefore, we’re going to apply erasure coding to itself. So how are we going to do that? Right here is one potential technique.
First, we take our 4-digit “file” and put it right into a 2×2 grid.
Then, we use the identical polynomial interpolation and extension course of as above to increase the file alongside each the x and y axes:
1 3 5 7 2 1 0 10 3 10 4 8
After which we apply the method once more to get the remaining 4 squares:
1 3 5 7 2 1 0 10 3 10 6 2 4 8 1 5
Be aware that it would not matter if we get the final 4 squares by increasing horizontally and vertically; as a result of secret sharing is linear it’s commutative with itself, so that you get the very same reply both method. Now, suppose we lose a quantity within the center, say, 6. Properly, we will do a restore vertically:
> share.restore([5, 0, None, 1], e) [5, 0, 6, 1]
Or horizontally:
> share.restore([3, 10, None, 2], e) [3, 10, 6, 2]
And tada, we get 6 in each instances. That is the shocking factor: the polynomials work equally nicely on each the x or the y axis. Therefore, if we take these 16 items from the grid, and break up them up amongst 16 nodes, and one of many nodes disappears, then nodes alongside both axis can come collectively and reconstruct the information that was held by that individual node and begin claiming the reward for storing that knowledge. Ideally, we will even lengthen this course of past 2 dimensions, producing a three-dimensional dice, a four-dimensional hypercube or extra – the acquire of utilizing extra dimensions is ease of reconstruction, and the fee is a decrease diploma of redundancy. Thus, what now we have is an information-theoretic equal of one thing that sounds prefer it got here straight out of science-fiction: a extremely redundant, interlinking, modular self-healing dice, that may shortly regionally detect and repair its personal errors even when massive sections of the dice have been to be broken, co-opted or destroyed.

“The dice can nonetheless operate even when as much as 78% of it have been to be destroyed…”
So, let’s put all of it collectively. You could have a ten GB file, and also you need to break up it up throughout the community. First, you encrypt the file, and then you definitely break up the file into, to illustrate, 125 chunks. You organize these chunks right into a three-dimensional 5x5x5 dice, determine the polynomial alongside every axis, and “lengthen” every one in order that on the finish you may have a 7x7x7 dice. You then search for 343 nodes keen to retailer every bit of information, and inform every node solely the id of the opposite nodes which are alongside the identical axis (we need to make an effort to keep away from a single node gathering collectively a complete line, sq. or dice and storing it and calculating any redundant chunks as wanted in real-time, getting the reward for storing all of the chunks of the file with out truly offering any redundancy.
With the intention to truly retrieve the file, you’ll ship out a request for the entire chunks, then see which of the items coming in have the best bandwidth. Chances are you’ll use the pay-per-chunk protocol to pay for the sending of the information; extortion will not be a problem as a result of you may have such excessive redundancy so nobody has the monopoly energy to disclaim you the file. As quickly because the minimal variety of items arrive, you’ll do the maths to decrypt the items and reconstitute the file regionally. Maybe, if the encoding is per-byte, you could even be capable to apply this to a Youtube-like streaming implementation, reconstituting one byte at a time.
In some sense, there’s an unavoidable tradeoff between self-healing and vulnerability to this type of faux redundancy: if components of the community can come collectively and get better a lacking piece to supply redundancy, then a malicious massive actor within the community can get better a lacking piece on the fly to supply and cost for faux redundancy. Maybe some scheme involving including one other layer of encryption on every bit, hiding the encryption keys and the addresses of the storers of the person items behind one more erasure code, and incentivizing the revelation course of solely at some explicit occasions may kind an optimum stability.
Secret Sharing
At the start of the article, I discussed one other identify for the idea of erasure coding, “secret sharing”. From the identify, it is easy to see how the 2 are associated: in case you have an algorithm for splitting knowledge up amongst 9 nodes such that 5 of 9 nodes are wanted to get better it however 4 of 9 cannot, then one other apparent use case is to make use of the identical algorithm for storing non-public keys – break up up your Bitcoin pockets backup into 9 components, give one to your mom, one to your boss, one to your lawyer, put three into just a few security deposit bins, and so forth, and when you neglect your password then you can ask every of them individually and chances are high at the least 5 gives you your items again, however the people themselves are sufficiently far aside from one another that they are unlikely to collude with one another. It is a very official factor to do, however there’s one implementation element concerned in doing it proper.
The difficulty is that this: although 4 of 9 cannot get better the unique key, 4 of 9 can nonetheless come collectively and have various details about it – particularly, 4 linear equations over 5 unknowns. This reduces the dimensionality of the selection house by an element of 5, so as a substitute of two256 non-public keys to look via they now have solely 251. In case your secret is 180 bits, that goes right down to 236 – trivial work for a fairly highly effective laptop. The way in which we repair that is by erasure-coding not simply the non-public key, however somewhat the non-public key plus 4x as many bytes of random gook. Extra exactly, let the non-public key be the zero-degree coefficient of the polynomial, choose 4 random values for the following 4 coefficients, and take values from that. This makes every bit 5 occasions longer, however with the profit that even 4 of 9 now have the whole alternative house of two180 or 2256 to look via.
Conclusion
So there we go, that is an introduction to the facility of erasure coding – arguably the only most underhyped set of algorithms (besides maybe SCIP) in laptop science or cryptography. The concepts right here basically are to file storage what multisig is to sensible contracts, permitting you to get the completely most potential quantity of safety and redundancy out of no matter ratio of storage overhead you’re keen to simply accept. It is an strategy to file storage availability that strictly supersedes the probabilities provided by easy splitting and replication (certainly, replication is definitely precisely what you get when you attempt to apply the algorithm with a 1-of-n technique), and can be utilized to encapsulate and individually deal with the issue of redundancy in the identical method that encryption encapsulates and individually handles the issue of privateness.
Decentralized file storage remains to be removed from a solved downside; though a lot of the core know-how, together with erasure coding in Tahoe-LAFS, has already been carried out, there are definitely many minor and not-so-minor implementation particulars that also should be solved for such a setup to truly work. An efficient status system will probably be required for measuring quality-of-service (eg. a node up 99% of the time is price at the least 3x greater than a node up 50% of the time). In some methods, incentivized file storage even relies on efficient blockchain scalability; having to implicitly pay for the charges of 343 transactions going to verification contracts each hour will not be going to work till transaction charges grow to be far decrease than they’re immediately, and till then some extra coarse-grained compromises are going to be required. However then once more, just about each downside within the cryptocurrency house nonetheless has a really lengthy option to go.

