
Time-series forecasting is a vital analysis space that’s essential to a number of scientific and industrial functions, like retail provide chain optimization, vitality and site visitors prediction, and climate forecasting. In retail use instances, for instance, it has been noticed that enhancing demand forecasting accuracy can meaningfully scale back stock prices and improve income.
Trendy time-series functions can contain forecasting tons of of 1000’s of correlated time-series (e.g., calls for of various merchandise for a retailer) over lengthy horizons (e.g., 1 / 4 or 12 months away at day by day granularity). As such, time-series forecasting fashions have to fulfill the next key criterias:
- Potential to deal with auxiliary options or covariates: Most use-cases can profit tremendously from successfully utilizing covariates, for example, in retail forecasting, holidays and product particular attributes or promotions can have an effect on demand.
- Appropriate for various information modalities: It ought to be capable of deal with sparse rely information, e.g., intermittent demand for a product with low quantity of gross sales whereas additionally having the ability to mannequin strong steady seasonal patterns in site visitors forecasting.
Quite a lot of neural community–based mostly options have been capable of present good efficiency on benchmarks and likewise assist the above criterion. Nevertheless, these strategies are sometimes sluggish to coach and may be costly for inference, particularly for longer horizons.
In “Lengthy-term Forecasting with TiDE: Time-series Dense Encoder”, we current an all multilayer perceptron (MLP) encoder-decoder structure for time-series forecasting that achieves superior efficiency on lengthy horizon time-series forecasting benchmarks when in comparison with transformer-based options, whereas being 5–10x sooner. Then in “On the advantages of most probability estimation for Regression and Forecasting”, we display that utilizing a fastidiously designed coaching loss perform based mostly on most probability estimation (MLE) may be efficient in dealing with completely different information modalities. These two works are complementary and may be utilized as part of the identical mannequin. In actual fact, they are going to be obtainable quickly in Google Cloud AI’s Vertex AutoML Forecasting.
TiDE: A easy MLP structure for quick and correct forecasting
Deep studying has proven promise in time-series forecasting, outperforming conventional statistical strategies, particularly for big multivariate datasets. After the success of transformers in pure language processing (NLP), there have been a number of works evaluating variants of the Transformer structure for lengthy horizon (the period of time into the long run) forecasting, corresponding to FEDformer and PatchTST. Nevertheless, different work has advised that even linear fashions can outperform these transformer variants on time-series benchmarks. Nonetheless, easy linear fashions aren’t expressive sufficient to deal with auxiliary options (e.g., vacation options and promotions for retail demand forecasting) and non-linear dependencies on the previous.
We current a scalable MLP-based encoder-decoder mannequin for quick and correct multi-step forecasting. Our mannequin encodes the previous of a time-series and all obtainable options utilizing an MLP encoder. Subsequently, the encoding is mixed with future options utilizing an MLP decoder to yield future predictions. The structure is illustrated under.
 |
| TiDE mannequin structure for multi-step forecasting. |
TiDE is greater than 10x sooner in coaching in comparison with transformer-based baselines whereas being extra correct on benchmarks. Related positive aspects may be noticed in inference because it solely scales linearly with the size of the context (the variety of time-steps the mannequin seems to be again) and the prediction horizon. Beneath on the left, we present that our mannequin may be 10.6% higher than the perfect transformer-based baseline (PatchTST) on a well-liked site visitors forecasting benchmark, when it comes to take a look at imply squared error (MSE). On the precise, we present that on the identical time our mannequin can have a lot sooner inference latency than PatchTST.
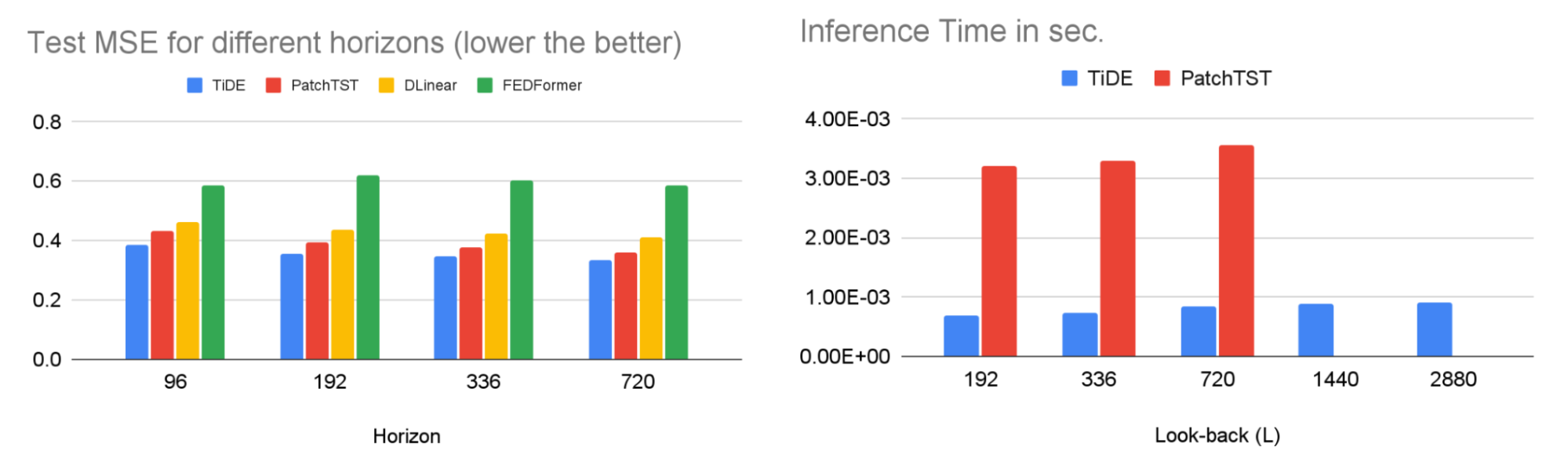 |
| Left: MSE on the take a look at set of a well-liked site visitors forecasting benchmark. Proper: inference time of TiDE and PatchTST as a perform of the look-back size. |
Our analysis demonstrates that we are able to reap the benefits of MLP’s linear computational scaling with look-back and horizon sizes with out sacrificing accuracy, whereas transformers scale quadratically on this state of affairs.
Probabilistic loss capabilities
In most forecasting functions the tip person is desirous about fashionable goal metrics just like the imply absolute proportion error (MAPE), weighted absolute proportion error (WAPE), and so on. In such eventualities, the usual method is to make use of the identical goal metric because the loss perform whereas coaching. In “On the advantages of most probability estimation for Regression and Forecasting”, accepted at ICLR, we present that this method won’t all the time be the perfect. As a substitute, we advocate utilizing the utmost probability loss for a fastidiously chosen household of distributions (mentioned extra under) that may seize inductive biases of the dataset throughout coaching. In different phrases, as a substitute of straight outputting level predictions that decrease the goal metric, the forecasting neural community predicts the parameters of a distribution within the chosen household that greatest explains the goal information. At inference time, we are able to predict the statistic from the discovered predictive distribution that minimizes the goal metric of curiosity (e.g., the imply minimizes the MSE goal metric whereas the median minimizes the WAPE). Additional, we are able to additionally simply get hold of uncertainty estimates of our forecasts, i.e., we are able to present quantile forecasts by estimating the quantiles of the predictive distribution. In a number of use instances, correct quantiles are important, for example, in demand forecasting a retailer would possibly wish to inventory for the ninetieth percentile to protect towards worst-case eventualities and keep away from misplaced income.
The selection of the distribution household is essential in such instances. For instance, within the context of sparse rely information, we would wish to have a distribution household that may put extra likelihood on zero, which is usually often known as zero-inflation. We suggest a mix of various distributions with discovered combination weights that may adapt to completely different information modalities. Within the paper, we present that utilizing a mix of zero and a number of damaging binomial distributions works properly in a wide range of settings as it may adapt to sparsity, a number of modalities, rely information, and information with sub-exponential tails.
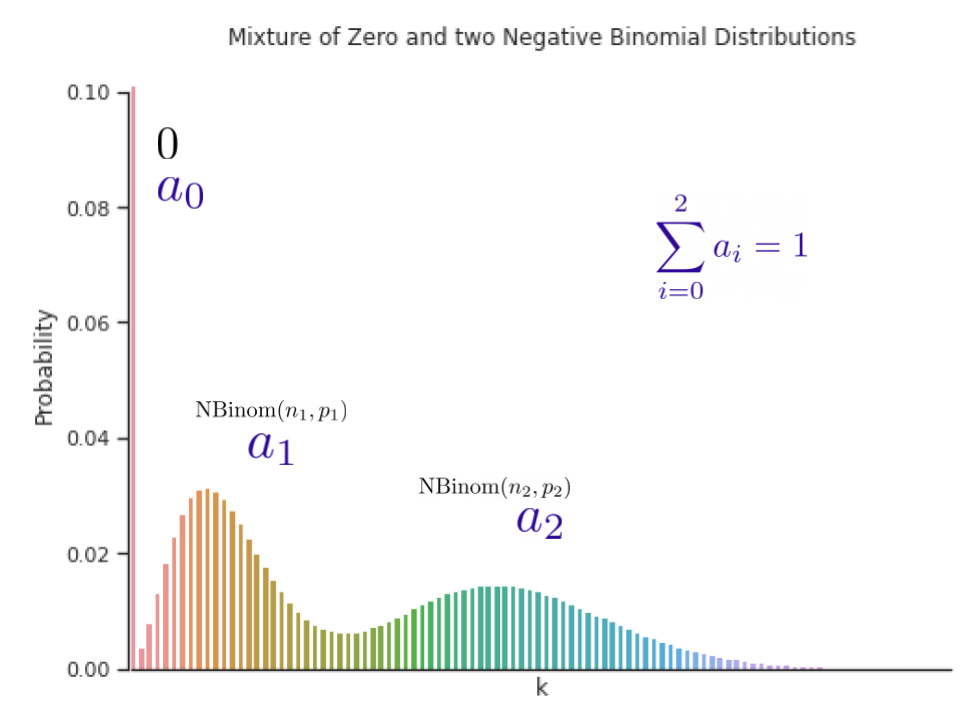 |
| A mix of zero and two damaging binomial distributions. The weights of the three elements, a1, a2 and a3, may be discovered throughout coaching. |
We use this loss perform for coaching Vertex AutoML fashions on the M5 forecasting competitors dataset and present that this straightforward change can result in a 6% acquire and outperform different benchmarks within the competitors metric, weighted root imply squared scaled error (WRMSSE).
| M5 Forecasting | WRMSSE |
| Vertex AutoML | 0.639 +/- 0.007 |
| Vertex AutoML with probabilistic loss | 0.581 +/- 0.007 |
| DeepAR | 0.789 +/- 0.025 |
| FEDFormer | 0.804 +/- 0.033 |
Conclusion
We’ve got proven how TiDE, along with probabilistic loss capabilities, allows quick and correct forecasting that robotically adapts to completely different information distributions and modalities and likewise offers uncertainty estimates for its predictions. It offers state-of-the-art accuracy amongst neural community–based mostly options at a fraction of the price of earlier transformer-based forecasting architectures, for large-scale enterprise forecasting functions. We hope this work will even spur curiosity in revisiting (each theoretically and empirically) MLP-based deep time-series forecasting fashions.
Acknowledgements
This work is the results of a collaboration between a number of people throughout Google Analysis and Google Cloud, together with (in alphabetical order): Pranjal Awasthi, Dawei Jia, Weihao Kong, Andrew Leach, Shaan Mathur, Petros Mol, Shuxin Nie, Ananda Theertha Suresh, and Rose Yu.

