Determine 1: stepwise conduct in self-supervised studying. When coaching widespread SSL algorithms, we discover that the loss descends in a stepwise vogue (high left) and the realized embeddings iteratively improve in dimensionality (backside left). Direct visualization of embeddings (proper; high three PCA instructions proven) confirms that embeddings are initially collapsed to some extent, which then expands to a 1D manifold, a 2D manifold, and past concurrently with steps within the loss.
It’s broadly believed that deep studying’s beautiful success is due partly to its capability to find and extract helpful representations of complicated information. Self-supervised studying (SSL) has emerged as a number one framework for studying these representations for pictures instantly from unlabeled information, just like how LLMs study representations for language instantly from web-scraped textual content. But regardless of SSL’s key function in state-of-the-art fashions corresponding to CLIP and MidJourney, elementary questions like “what are self-supervised picture programs actually studying?” and “how does that studying really happen?” lack primary solutions.
Our latest paper (to seem at ICML 2023) presents what we advise is the primary compelling mathematical image of the coaching technique of large-scale SSL strategies. Our simplified theoretical mannequin, which we clear up precisely, learns points of the information in a sequence of discrete, well-separated steps. We then exhibit that this conduct will be noticed within the wild throughout many present state-of-the-art programs.
This discovery opens new avenues for bettering SSL strategies, and permits a complete vary of latest scientific questions that, when answered, will present a strong lens for understanding a few of at present’s most essential deep studying programs.
Background
We focus right here on joint-embedding SSL strategies — a superset of contrastive strategies — which study representations that obey view-invariance standards. The loss perform of those fashions features a time period implementing matching embeddings for semantically equal “views” of a picture. Remarkably, this easy strategy yields highly effective representations on picture duties even when views are so simple as random crops and colour perturbations.
Principle: stepwise studying in SSL with linearized fashions
We first describe an precisely solvable linear mannequin of SSL by which each the coaching trajectories and closing embeddings will be written in closed type. Notably, we discover that illustration studying separates right into a sequence of discrete steps: the rank of the embeddings begins small and iteratively will increase in a stepwise studying course of.
The primary theoretical contribution of our paper is to precisely clear up the coaching dynamics of the Barlow Twins loss perform underneath gradient stream for the particular case of a linear mannequin (mathbf{f}(mathbf{x}) = mathbf{W} mathbf{x}). To sketch our findings right here, we discover that, when initialization is small, the mannequin learns representations composed exactly of the top-(d) eigendirections of the featurewise cross-correlation matrix (boldsymbol{Gamma} equiv mathbb{E}_{mathbf{x},mathbf{x}’} [ mathbf{x} mathbf{x}’^T ]). What’s extra, we discover that these eigendirections are realized separately in a sequence of discrete studying steps at occasions decided by their corresponding eigenvalues. Determine 2 illustrates this studying course of, displaying each the expansion of a brand new course within the represented perform and the ensuing drop within the loss at every studying step. As an additional bonus, we discover a closed-form equation for the ultimate embeddings realized by the mannequin at convergence.
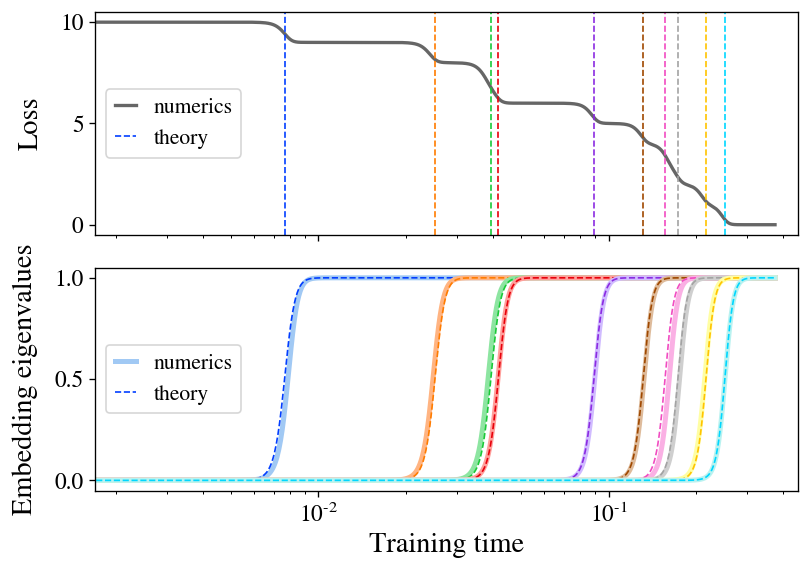
Determine 2: stepwise studying seems in a linear mannequin of SSL. We practice a linear mannequin with the Barlow Twins loss on a small pattern of CIFAR-10. The loss (high) descends in a staircase vogue, with step occasions well-predicted by our idea (dashed traces). The embedding eigenvalues (backside) spring up separately, intently matching idea (dashed curves).
Our discovering of stepwise studying is a manifestation of the broader idea of spectral bias, which is the statement that many studying programs with roughly linear dynamics preferentially study eigendirections with greater eigenvalue. This has lately been well-studied within the case of ordinary supervised studying, the place it’s been discovered that higher-eigenvalue eigenmodes are realized quicker throughout coaching. Our work finds the analogous outcomes for SSL.
The rationale a linear mannequin deserves cautious research is that, as proven through the “neural tangent kernel” (NTK) line of labor, sufficiently extensive neural networks even have linear parameterwise dynamics. This reality is ample to increase our resolution for a linear mannequin to extensive neural nets (or actually to arbitrary kernel machines), by which case the mannequin preferentially learns the highest (d) eigendirections of a selected operator associated to the NTK. The research of the NTK has yielded many insights into the coaching and generalization of even nonlinear neural networks, which is a clue that maybe a few of the insights we’ve gleaned would possibly switch to sensible circumstances.
Experiment: stepwise studying in SSL with ResNets
As our important experiments, we practice a number of main SSL strategies with full-scale ResNet-50 encoders and discover that, remarkably, we clearly see this stepwise studying sample even in sensible settings, suggesting that this conduct is central to the educational conduct of SSL.
To see stepwise studying with ResNets in sensible setups, all we have now to do is run the algorithm and monitor the eigenvalues of the embedding covariance matrix over time. In apply, it helps spotlight the stepwise conduct to additionally practice from smaller-than-normal parameter-wise initialization and practice with a small studying price, so we’ll use these modifications within the experiments we discuss right here and focus on the usual case in our paper.
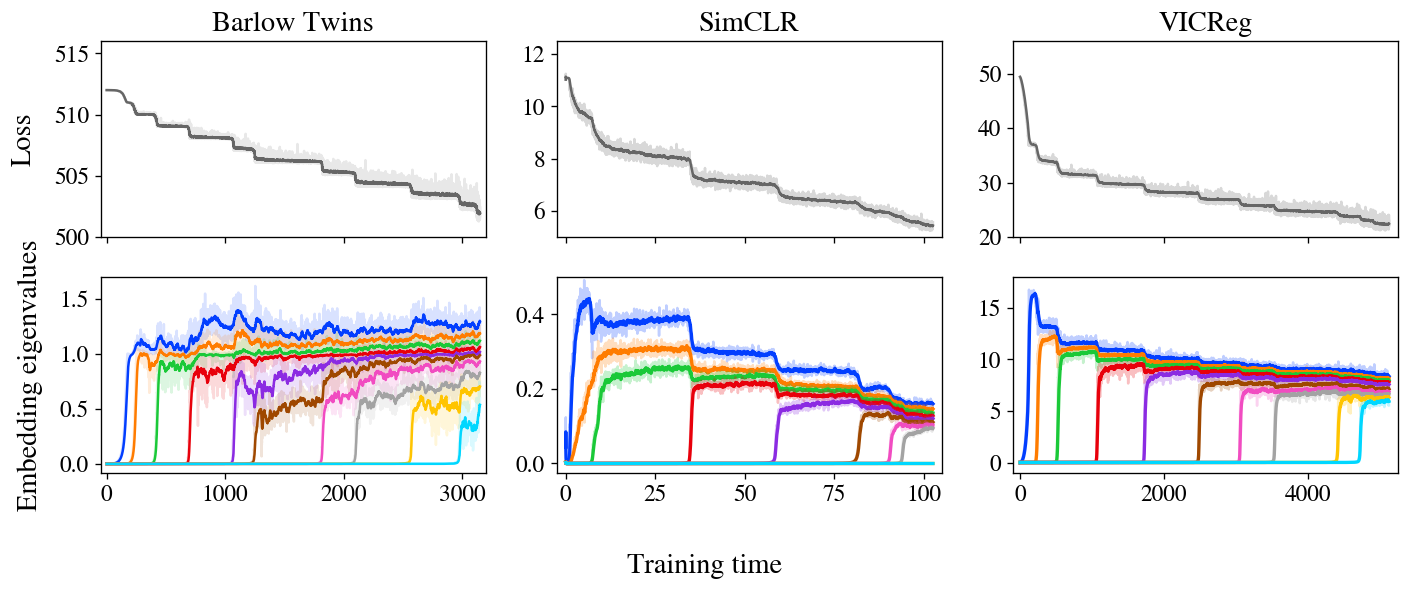
Determine 3: stepwise studying is clear in Barlow Twins, SimCLR, and VICReg. The loss and embeddings of all three strategies show stepwise studying, with embeddings iteratively rising in rank as predicted by our mannequin.
Determine 3 reveals losses and embedding covariance eigenvalues for 3 SSL strategies — Barlow Twins, SimCLR, and VICReg — skilled on the STL-10 dataset with customary augmentations. Remarkably, all three present very clear stepwise studying, with loss reducing in a staircase curve and one new eigenvalue arising from zero at every subsequent step. We additionally present an animated zoom-in on the early steps of Barlow Twins in Determine 1.
It’s value noting that, whereas these three strategies are slightly totally different at first look, it’s been suspected in folklore for a while that they’re doing one thing related underneath the hood. Particularly, these and different joint-embedding SSL strategies all obtain related efficiency on benchmark duties. The problem, then, is to determine the shared conduct underlying these assorted strategies. A lot prior theoretical work has centered on analytical similarities of their loss capabilities, however our experiments recommend a unique unifying precept: SSL strategies all study embeddings one dimension at a time, iteratively including new dimensions so as of salience.
In a final incipient however promising experiment, we evaluate the actual embeddings realized by these strategies with theoretical predictions computed from the NTK after coaching. We not solely discover good settlement between idea and experiment inside every methodology, however we additionally evaluate throughout strategies and discover that totally different strategies study related embeddings, including additional help to the notion that these strategies are finally doing related issues and will be unified.
Why it issues
Our work paints a primary theoretical image of the method by which SSL strategies assemble realized representations over the course of coaching. Now that we have now a idea, what can we do with it? We see promise for this image to each support the apply of SSL from an engineering standpoint and to allow higher understanding of SSL and doubtlessly illustration studying extra broadly.
On the sensible aspect, SSL fashions are famously sluggish to coach in comparison with supervised coaching, and the rationale for this distinction isn’t identified. Our image of coaching means that SSL coaching takes a very long time to converge as a result of the later eigenmodes have very long time constants and take a very long time to develop considerably. If that image’s proper, dashing up coaching can be so simple as selectively focusing gradient on small embedding eigendirections in an try to tug them as much as the extent of the others, which will be carried out in precept with only a easy modification to the loss perform or the optimizer. We focus on these prospects in additional element in our paper.
On the scientific aspect, the framework of SSL as an iterative course of permits one to ask many questions on the person eigenmodes. Are those realized first extra helpful than those realized later? How do totally different augmentations change the realized modes, and does this rely on the precise SSL methodology used? Can we assign semantic content material to any (subset of) eigenmodes? (For instance, we’ve observed that the primary few modes realized typically characterize extremely interpretable capabilities like a picture’s common hue and saturation.) If different types of illustration studying converge to related representations — a reality which is well testable — then solutions to those questions might have implications extending to deep studying extra broadly.
All thought of, we’re optimistic in regards to the prospects of future work within the space. Deep studying stays a grand theoretical thriller, however we imagine our findings right here give a helpful foothold for future research into the educational conduct of deep networks.
This put up relies on the paper “On the Stepwise Nature of Self-Supervised Studying”, which is joint work with Maksis Knutins, Liu Ziyin, Daniel Geisz, and Joshua Albrecht. This work was performed with Typically Clever the place Jamie Simon is a Analysis Fellow. This blogpost is cross-posted right here. We’d be delighted to discipline your questions or feedback.
